Zamiast wstępu chciałbym napisać, co będę nazywał naukami przyrodniczymi. Za takie powszechnie uznaje się fizykę, chemię, biologię i ich skrzyżowania. Ja jednak będę pisał głównie o fizyce, ponieważ wydaje mi się to słuszne z dwóch powodów. Po pierwsze, fizyka bada świat na jego najbardziej fundamentalnym poziomie, takim jak struktura atomu, oraz w skali kosmicznej — galaktyk i ich wielkoskalowych struktur, daje więc pełny obraz świata. Po drugie, u podstaw biologii leży chemia, a chemia jest właściwie działem fizyki, więc fizyka mówi nam coś o biologii, ale biologia o fizyce już nie. Dlatego fizyka jako najbardziej podstawowa jest nauką „najbardziej przyrodniczą".

Aby odpowiedzieć na tytułowe pytanie, należy najpierw zająć się jego pierwszą częścią, a więc rozważyć, czy nauka w ogóle mówi nam coś o świecie rzeczywistym. Już samo określenie „świat rzeczywisty" sprawia tu problem, choćby dlatego, że być może nie ma możliwości odróżnienia świata rzeczywistego od wyimaginowanego, pozornego itp. Wystarczy wspomnieć tu ideę mózgu w naczyniu Putnama [1]: może postrzegany przez nas świat istnieje zależnie od innego, jest jego częścią. Może za nasze odczucia i wrażenia zmysłowe odpowiada program komputerowy napisany przez jakieś wyższe istoty, a my sami, podobnie jak nasze wrażenia i cały nasz Wszechświat, jesteśmy częścią tego programu. Nie mamy żadnej możliwości empirycznego stwierdzenia, czy tak jest w istocie.

Zagadnienie to wymagałoby znacznie szerszego omówienia, które wykraczałoby poza granice tematu. Założę więc, że nawet, jeśli taka sytuacja zachodzi, to nasz Wszechświat w jakiś sposób (umownie powiedzmy, że rzeczywiście) istnieje. Jednak istnienie rzeczywistego świata nie implikuje możliwości jego badania, poznania i opisu przez naukę. Istniejący Wszechświat musi spełniać szereg kryteriów, by móc być badanym. Pierwszym i najważniejszym, choć często zapominanym, warunkiem jest istnienie kogoś, kto mógłby postrzegać dany Wszechświat. Nakłada to silne ograniczenia na wartości wielu stałych fizycznych, ale najwyraźniej istnieje co najmniej jeden zestaw tych stałych (i praw fizyki), który umożliwia powstanie inteligentnego życia we Wszechświecie. Wiemy to po prostu stąd, że istniejemy.

Nawet istnienie inteligencji we Wszechświecie nie implikuje jego poznawalności. Wszechświat nie byłby poznawalny bez pewnej cechy, która sprawia, że można go racjonalnie (bo jak inaczej) badać. Ponadto, aby istniejące istoty mogły badać Wszechświat, muszą same być racjonalne, a ich racjonalność musi odpowiadać racjonalności Wszechświata, jakoś z nią współgrać. To akurat nie wydaje się dużym problemem, ponieważ racjonalność powstaje razem z życiem w procesie ewolucji. A skoro powstaje w ten sposób, to musi jakoś ułatwiać reprodukcję, ponieważ tak właśnie działa ewolucja. A skoro tak, to ludzka (ograniczmy się do tego gatunku, jako jedynego znanego inteligentnego badacza naszego Wszechświata) racjonalność musi mieć jakiś związek z racjonalnością Wszechświata, bo inaczej do niczego by się nam nie przydała. Bardziej nieprawdopodobne wydaje się to, że nasza racjonalność pozwala nam na zrozumienie rzeczy nieprzydatnych w życiu codziennym, jak budowa jądra atomowego lub struktura czasoprzestrzeni.

Za tym, że nasz Wszechświat spełnia te wszystkie warunki, przemawia tylko skuteczność nauki w przewidywaniu zjawisk w nim zachodzących. Jednak przekonanie o tym, że skuteczność metody potwierdza założenia, na jakich metoda ta się opiera, jest niezgodne z zasadami logiki matematycznej, a więc jest nieracjonalne (choć niekoniecznie nieprawdziwe). Stąd prosty wniosek, że uznanie świata za możliwy do badania lub racjonalny jest nieracjonalne. W tym kontekście różni naukowcy mówili o „niezrozumiałej zrozumiałości świata".

Sama metoda jest również interesująca. Od czasów Newtona, a więc od trzech stuleci, nauka korzysta z metody matematyczno-empirycznej, która najwyraźniej jest skuteczna, na co wskazuje wykładnicze tempo narastania naszej wiedzy o świecie.

Jak sama nazwa wskazuje, metoda ta łączy matematykę i doświadczenie. Doświadczenie spełnia kluczową rolę w naszym poznaniu świata, i to z dwóch powodów. Przede wszystkim, nowe teorie fizyczne należy weryfikować empirycznie, by przekonać się o ich „prawdziwości". Jest to powszechnie uznawana doktryna: jeżeli dana teoria przewiduje zjawiska niewystępujące w przyrodzie, to należy ją zmodyfikować lub porzucić. Możliwość doświadczalnej weryfikacji teorii jest tak ważna, że została uznana za kryterium naukowości pracy. Jeśli jakieś twierdzenie naukowe nie może zostać zweryfikowane, nie jest ono częścią nauki. To kryterium naukowości, nazywane kryterium falsyfikowalności, zostało sformułowane przez Karla Poppera. W nieco ściślejszym ujęciu polega ono na tym, że dana teoria jest naukowa tylko wtedy, gdy istnieje możliwość przeprowadzenia eksperymentu, który tę teorię obali.

Kolejna, nie mniej ważna dla poznania świata, rola doświadczenia w nauce polega na inspirowaniu badaczy do tworzenia nowych teorii, które opisują świat lepiej, niż stare. Teoretycy ożywiają się z reguły wtedy, gdy zaobserwowane zostanie zjawisko nieprzewidywane przez aktualne teorie. Tak powstała mechanika kwantowa, chyba najbardziej znana i najmniej rozumiana część fizyki. Kilka prostych zjawisk, jak efekt fotoelektryczny, promieniowanie ciała doskonale czarnego czy dyfrakcja i interferencja elektronów, doprowadziły do przewrotu w fizyce, który trwa już od kilkudziesięciu lat.

Część matematyczna metody naukowej jest równie ważna. Ciekawe jest, że tak jak nie ma żadnego wyraźnego powodu, dla którego Wszechświat miałby być racjonalnie badalny, tak nie musi on również być badalny matematycznie. Zauważmy, że nawet, jeśli Wszechświat miałby tę dziwną cechę, która umożliwiałaby jego poznanie, nie miałby żadnego powodu, by poddawać się badaniu metodą właśnie matematyczną. Jak napisałem wyżej, jedyny powód, by uznać metodę matematyczną za właściwszą od innych, jest jej niesamowita skuteczność. Jest ona szokująca, jeśli weźmie się pod uwagę, jak silne warunki musi spełniać Wszechświat, by być badalnym metodami matematycznymi. Nawet jeśli jest on poznawalny, to i tak musi spełniać szereg kolejnych warunków, byśmy mogli opisywać go matematycznie.

Przede wszystkim dana przyroda musi być matematyzowalna, opisywalna jakąś matematyką. Być może istnieją (przynajmniej potencjalne) światy, które nie spełniają tego warunku, jednak wyobrażenie ich sobie przekracza moje możliwości.

Po drugie, matematyka opisująca świat musi być poznawczo dostępna dla podmiotu uprawiającego naukę. Nie ma żadnego powodu, dla którego moglibyśmy twierdzić, że jesteśmy w stanie zrozumieć wszystkie struktury matematyczne. Mózg ludzki, jak każda sieć neuronowa, ma skończoną pamięć oraz moc obliczeniową, więc niektóre struktury mogą być dla nas po prostu zbyt skomplikowane.

Nawet zasadniczo zrozumiała dla nas struktura matematyczna musi być dostatecznie prosta, byśmy mogli ją zauważyć. Z prawa grawitacji Newtona mówiącego, że siła grawitacji działająca między dwoma ciałami jest odwrotnie proporcjonalna do kwadratu ich wzajemnej odległości wynika, że orbity planet są elipsami. Eliptyczność orbit zauważył już Kepler, nie znając prawa grawitacji. Gdyby jednak wykładnik potęgi przy odległości nie był równy 2, ale 2,01, orbity te byłyby tak skomplikowane, że raczej nikt nie zauważyłby w nich żadnej prawidłowości.

Aby „opłacało się" tworzyć teorie fizyczne, muszą one jakoś upraszczać nasz opis świata. Na przykład wspomniane przed chwilą prawo powszechnego ciążenia Newtona nie podaje wartości siły grawitacji dla każdej możliwej odległości i iloczynu mas z osobna, a ujmuje te parametry w bardzo prosty wzór: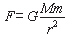

(G jest uniwersalną stałą, M i m to masy oddziałujących ciał, a r jest wzajemną odległością tych ciał). Wszechświat nie musi jednak zachowywać się w tak przyjemny dla nas sposób. Wyobraźmy sobie jakiś prosty świat, który może znajdować się w trzech stanach: a, b i c. Jego historia może być dana jakimś prostym ciągiem, na przykład ...abcabcabcabc... Widać wyraźnie, że ciąg ten można opisać trywialnie prostym wzorem. Natomiast w ogólnym przypadku ciąg reprezentujący historię świata może nie być przedstawialny regułą krótszą od samego ciągu — mówiąc językiem technicznym, nie musi być algorytmicznie ścieśnialny. Wtedy najprostszym sposobem opisu Wszechświata byłoby po prostu podanie jego historii, która może być na to zbyt bogata lub długa.

Na czym jednak dokładnie polega metoda matematyczna? Sprowadza się ona do tworzenia modeli matematycznych naszego świata. Modele te są pewnymi strukturami, w których pewne określone obiekty odpowiadają pewnym określonym mierzalnym wielkościom w świecie fizycznym. Właśnie te obiekty odpowiadają za możliwość eksperymentalnej weryfikacji teorii. Teoria fizyczna jest tym „lepsza", im lepiej przybliża strukturę świata w danym jej obszarze. Póki co wszystkie teorie są tylko przybliżeniami, bo żadna nie opisuje świata w całości. Na przykład ogólna teoria względności opisuje siły grawitacji w skali makroskopowej, ale pomija efekty kwantowe. Z kolei mechanika kwantowa opisuje zachowanie bardzo małych obiektów, ale nie uwzględnia grawitacji. Od pewnego czasu obserwuje się w fizyce silne dążenie do unifikacji teorii, do opisywania jak największej części struktury świata w jak najprostszy sposób. Tak powstała teoria elektromagnetyzmu Maxwella, a później teoria oddziaływań elektrosłabych, łącząca teorię Maxwella z teorią słabych oddziaływań jądrowych. Udało się też połączyć ogólną teorię względności z elektromagnetyzmem (teoria Kaluzy-Kleina) oraz szczególną teorię względności (opisującą układy w ruchu) z mechaniką kwantową (Dirac). Niestety jak dotąd nie powstała żadna teoria łącząca wszystkie oddziaływania i uwzględniająca efekty kwantowe, a wydaje się, że właśnie ona będzie kolejnym krokiem do kompletnego opisania Wszechświata. Na razie musimy zadowolić się teoriami opisującymi jedynie niektóre aspekty struktury świata. Oczywiście żadna część tej struktury nie istnieje niezależnie od innych, więc przewidywania takich „fragmentarycznych" teorii nie są dokładne.

W każdym rozumowaniu matematycznym przyjmuje się pewne aksjomaty, na których opiera się wywód. Fizyka nie jest, a przynajmniej nie powinna być, ograniczona żadnymi przyjętymi a priori założeniami — odrzucenie jednego z najbardziej oczywistych aksjomatów teorii Euklidesa doprowadziło do powstania ogólnej teorii względności. Problemem jest twierdzenie Gödla. Mówi ono, że żaden system sformalizowany zawierający arytmetykę nie może być jednocześnie zupełny i niesprzeczny, tzn. albo wystąpią w nim sprzeczności, albo pozostaną twierdzenia, których nie da się udowodnić lub obalić na podstawie przyjętych aksjomatów. Twierdzenie to odnosi się tylko do systemów sformalizowanych, do których teorie fizyczne są podobne tylko w pewnym stopniu. Nie wiadomo więc na razie, czy ograniczy ono rozwój fizyki. Póki co, pozostaje tylko poczekać i zobaczyć.

Istotny jest również stosunek teorii fizycznych do ich interpretacji. Co równania składające się na daną teorię mówią nam o świecie? Z fizycznego punktu widzenia istnieją tylko rozwiązania tych równań, natomiast przyporządkowanie tym rozwiązaniom konkretnych elementów postrzeganego przez nas świata jest już kwestią filozofii, a konkretnie ontologicznej interpretacji teorii. Właśnie ta interpretacja mówi nam, że to elektron i pozyton są tym czymś, co dostajemy rozwiązując równanie Diraca. Szczególnie istotne jest to w mechanice kwantowej. Wbrew temu, co piszą autorzy książek popularnonaukowych, teoria ta daje przewidywania w pełni deterministyczne, a dopiero ontologiczna interpretacja tych przewidywań daje losowość i indeterminizm.

Nieco wyżej napisałem, że świat badamy racjonalnie, „bo jak inaczej". Spotkałem się z kilkoma pomysłami nieracjonalnego badania świata, z których żaden nie wydał mi się obiecujący. Jeden z nich, podobny pod wieloma względami do innych, to tzw. „teoria splątań". Główne założenie tej teorii jest proste: logika jest nieprzydatna. Jeśli w poprawnym rozumowaniu dostajemy sprzeczność, to nic złego się nie stało, a założenia nadal mogą być prawdziwe. Moim zdaniem tego typu teorie są nieprzydatne, a najczęściej po prostu głupie. Dlatego właśnie uważam, że Wszechświat można badać tylko racjonalnie.

Literatura

[1] H. Putnam, Reason, Truth, and History, Cambridge University Press, 1981
[2] Prace Michała Hellera przedrukowane w książce pt. Filozofia i Wszechświat (Universitas, 2006):
· Czy świat jest racjonalny?
· Czy świat jest matematyczny?
· O języku fizyki
· Jak możliwa jest fizyka — Dum Deus calculat...
[3] M. Heller, Filozofia nauki. Wprowadzenie, Petrus, 2009

Po przeczytaniu tego tekstu, czytelnicy często wybierają też: Czy w nauce jest dyskryminacja kobiet? Wiara a rozum

Dodaj komentarz do strony..   Zobacz komentarze (8)..

Wyślij mailem..

Wersja do druku    PDF    MS Word