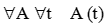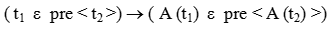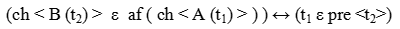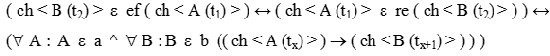Rozważmy teraz problem wzajemnej zależności czasu i obiektów. Leśniewski nie skupia się na czasie, ale na obiektach, znajdujących się w systemie. Chcąc powiększyć system o czas, musimy uwzględnić relację, w jaką będzie on wchodził z obiektami. Naszym celem jest zaznaczenie, że obiekt istnieje w czasie. Zapiszmy to w następujący sposób A (t). Narzuca to oczywiste skojarzenie z funkcją. Zmiennymi niezależnymi będą zatem momenty czasu (np. t1, t2, t3,...), natomiast stany obiektów staną się zmiennymi zależnymi (będą nimi: A (t1), A (t2), A (t3)). Wróćmy jeszcze do problemu istnienia obiektów w czasie. Przyjęliśmy już model dyskretny, ale czy to wystarczy, aby wyeliminować wszystkie trudności. Przypuśćmy, że mamy trzy kolejne momenty czasu: t1, t2, t3. Wyobraźmy sobie, że obiekt A (t1) chcemy przekształcić w obiekt A', ale przekształcenie to zajmie nam 2*(delta)t, gdzie (delta)t = t2 — t1 = t3 — t2. Zatem zmiana będzie przekształcać A (t1) na A (t3). Co zatem dzieje się z obiektem A w czasie t2? Nie możemy przyjąć, że obiekt nie istnieje, bowiem wtedy nie miałoby sensu tworzenie modelu dyskretnego, model ciągły w zupełności by wystarczył. Zatem obiekt musi istnieć, ale w ten sposób wracalibyśmy do problemu, od którego również próbowaliśmy się już uwolnić. Odpowiedź jest bardzo prosta: takie przekształcenie nie może istnieć. Czyli dla każdego czasu, dla każdego obiektu istnieje jednoznaczne określenie tego obiektu w tym czasie. Określenie to będzie funkcją. Sformułujmy więc drugi aksjomat chronologii:
(A2)

Drugi aksjomat pociąga za sobą konieczność wprowadzenia jeszcze jednego, który by to przyporządkowanie określał. Musimy bowiem zaznaczyć kierunek upływu czasu. Dlatego należy zaznaczyć, że jeżeli dany czas t1 jest wcześniejszy od t2, to obiekt znajdujący się w czasie t1 jest wcześniejszy od tego samego obiektu w czasie t2. Wprowadzimy tu nowe oznaczenia. Pierwszym z nich będzie symbol „pre <x>", czyli bycie wcześniejszym niż dany x, drugim symbol "x e y" mówiący, że „x jest y". Możemy teraz sformułować trzeci aksjomat chronologii:
(A3)

Posiadamy teraz pełną aksjomatykę chronologii. Możemy przystąpić do formułowania podstawowych definicji. Wiemy już, czym jest zmiana obiektu w czasie (ch < A (t1) >). Jest to przekształcenie tego obiektu w obiekt A (t2). Poznaliśmy także symbol pre <x>. Chronologia otwiera również możliwość rozpatrywania problemów: przyczyna — skutek czy następstwo wydarzeń. Przedstawię teraz ich definicje. Zacznijmy od następstwa wydarzeń, przypiszemy mu symbol af <x>. O następstwie wydarzeń możemy mówić, gdy jedna zmiana obiektu zacznie się po zakończeniu zmiany drugiego obiektu. Zatem:

Definicja (następstwo wydarzeń — af <x>):

Na wszelki wypadek podajmy jeszcze jej słowny zapis: zmiana obiektu B w czasie t2 jest następstwem zmiany obiektu A w czasie t1, wtedy i tylko wtedy, gdy czas t1 jest wcześniejszy od czasu t2.

Definicja następstwa wydarzeń jest w miarę prosta. Chcąc zdefiniować przyczynę i skutek, musimy odwołać się do powyższej definicji oraz zaznaczyć, że wydarzenia następujące po sobie są jakiś sposób powiązane. Wprowadźmy więc tu rodzaj obiektów "a" (piszemy "A e a", aby powiedzieć „A jest rodzaju a"). Umożliwi nam to powiązanie pewnych zjawisk poprzez określenie, że każdy obiekt pewnego rodzaju zmienia się w jakiś określony sposób pod wpływem zmiany każdego obiektu innego określonego rodzaju. Zatem:

Definicja (przyczyna — re <x> i skutek — ef <x>):

A oto jej słowny zapis: Zmiana obiektu B w czasie t2 jest skutkiem zmiany obiektu A w czasie t1 wtedy i tylko wtedy, gdy zmiana obiektu A w czasie t1 jest przyczyną zmiany obiektu B w czasie t2, a to ma miejsce wtedy i tylko wtedy, gdy dla każdego obiektu A będącego pewnego rodzaju a i dla każdego obiektu B będącego pewnego rodzaju b, zmiana obiektu A w czasie tx powoduje zmianę obiektu B w czasie tx+1.

Przedstawiony tu projekt „czwartego" systemu oczywiście wymaga jeszcze dalszego dopracowania. Czy jego podjęcie ma jednak sens? Bowiem...

Wydawało mi się, że próba sformalizowania pewnych problemów metafizycznych może przyczynić się do lepszego zrozumienia sposobu funkcjonowania naszego umysłu. Poznając świat przecież w jakiś sposób kodujemy zdobywane informacje, tworzymy pewien mniej lub bardziej świadomy system reprezentacji świata. Mam jednak coraz więcej wątpliwości (przedstawienie ich wymaga jednak osobnego eseju), czy nasze sieci neuronalne mogą przechowywać informacje w postaci wyżej zarysowanych systemów. No cóż, naukowiec może być martwy już za życia i jest w tym coś bardzo pocieszającego, może bowiem narodzić się ponownie.

1. R. Courant, H. Robins, Co to jest matematyka?, Warszawa 1967
2. K. Devlin, Żegnaj Kartezjuszu, Warszawa 1999
3. G. Edelman, Przenikliwe powietrze, jasny ogień, Warszawa 1998
4. E. Nieznański, Logika. Podstawy — język — uzasadnienie. Warszawa 2000
5. J. Stuchliński, Definicja zdania prawdziwego w językach logiki i w językach opartych na logice, Warszawa 2002

Po przeczytaniu tego tekstu, czytelnicy często wybierają też: Wprowadzenie do chaosu O szkodliwości logiki

Dodaj komentarz do strony..   Zobacz komentarze (1)..

Wyślij mailem..

Wersja do druku    PDF    MS Word