
|
Nauka » Astronomia » Budujemy własny teleskop Figuryzacja zwierciadła - niezbędna teoria Tylko idealne warunki pracy doprowadzą do powstania zwierciadła o kształcie sferycznym bliskim doskonałości za pomocą powyższych metod. W świecie rzeczywistym zwierciadło zwykle posiada błędy powierzchni i wymaga korekcji. Jedynym zwierciadłem, którego kształtu nie można poprawić, to takie które spadło na podłogę i roztrzaskało się na kawałki. Celem figuryzacji zwierciadła jest doprowadzenie go do kształtu sferycznego, następnie parabolizacja, choć nie jest to absolutnie niezbędne. Ja uzyskałem kształt paraboidalny bez figuryzacji na sferę. Jednak trzymajmy się metody standardowej, która wiedzie poprzez sferę. Do figuryzacji zwierciadła będzie potrzebny kolejny rodzaj testu, jednak zanim poznamy jego tajniki, niezbędne jest zapoznanie się z podstawami optyki, które postaram się przedstawić jak najzwięźlej. Chciałbym ograniczyć to do absolutnego minimum i nie odchodzić od zagadnienia optyki zwierciadeł wklęsłych. Niezbędnym jest jednak zrozumienie poniższych informacji, inaczej dalsze studia nad zwierciadłem staną się niejasne. Jeśli ktoś postanowi pogłębić swoją wiedzę, zapraszam do literatury i książek poświęconych optyce. Ja przedstawiam jedynie informacje dla osoby, która chce stworzyć swoje zwierciadło, bez grzebania się w skomplikowanych wzorach i zagadnieniach. Aby zwierciadło teleskopu skupiało światło pochodzące z nieskończoności w jednym punkcie, musi posiadać kształt paraboidalny. Jeśli zwierciadło będzie wycinkiem sfery, promienie odbite od jego krawędzi zostaną skupione nieco bliżej wzdłuż osi optycznej, niż promienie odbite od jego środka. Pozostawanie przy kształcie sferycznym jest błędem i swojego rodzaju pójściem na łatwiznę. Nie po to pracujemy ciężko tyle czasu, aby uzyskać zwierciadło o wątpliwej jakości. Tutaj nie ma mowy o kompromisach, jeśli nie jesteś perfekcjonistą, w ogóle nie zabieraj się za szlifowanie zwierciadła. Sfera to jest etap przejściowy, z którego rozpoczyna się proces parabolizacji. Obecnie istnieje doskonałe oprogramowanie, które pozwala na figuryzację paraboli z ogromną dokładnością, bez znajomości skomplikowanych wzorów i profesjonalnej wiedzy. Aby usunąć defekt zwierciadła sferycznego, czyli zrównać światło skupione z krawędzi i środka, należy je odpowiednio zmodyfikować. W tym celu należy nieco pogłębić środek zwierciadła (aby przybliżyć punkt skupienia promieni wewnętrznych) i spłaszczyć jego krawędź (aby oddalić punkt skupienia promieni marginalnych). Gdy przełożymy to na regularną, matematyczną figurę, uzyskamy właśnie kształt paraboidalny. Spójrz na schemat poniżej. 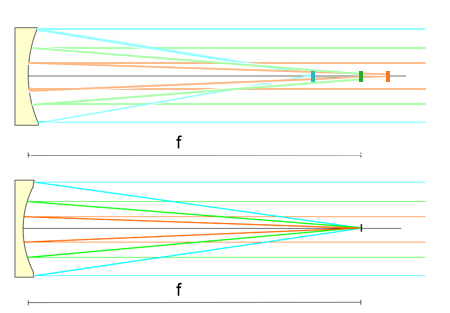 Rycina 39. Porównanie właściwości zwierciadła sferycznego (na górze) i paraboidalnego (dół). W przypadku zwierciadła sferycznego, promienie dochodzące z nieskończoności padają w różnych punktach na osi optycznej. Zjawisko to nazywa się aberracją sferyczną. W przypadku zwierciadła paraboidalnego, promienie skupiają się w jednym punkcie, którego odległość od zwierciadła jest określana długością ogniskową. Dlatego też najlepsze obrazy można uzyskać wyłącznie w drugim przypadku. Jak jednak możemy określić rzeczywisty kształt zwierciadła? Nikt nie jest w stanie ocenić na oko, gdzie dokładnie skupione jest światło padające na zwierciadło. Zatem czas zapoznać się z drugą ciekawą właściwością zwierciadła sferycznego i paraboidalnego. Jeśli źródło światła znajduje się w blisko zwierciadła, sytuacja wygląda zupełnie odwrotnie. Zwierciadło sferyczne skupia wtedy światło w jednym punkcie, zwierciadło paraboidalne zaś skupia promienie w różnych punktach na osi optycznej. 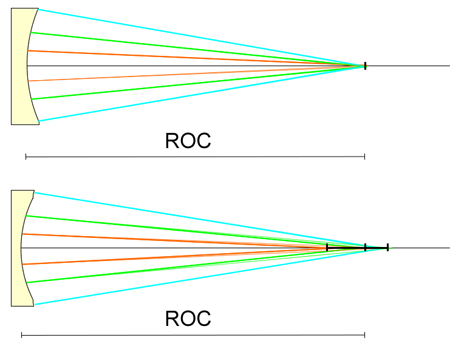 Rycina 40. Porównanie właściwości zwierciadła sferycznego (na górze) i paraboidalnego (dół). Kiedy umieścimy źródło światła blisko zwierciadła, następuje zupełna zamiana właściwości zwierciadeł sferycznego i paraboidalnego. Zwierciadło sferyczne skupia promienie bliskie w jednym punkcie, zwierciadło paraboidalne w różnych. Promienie są wysyłane i skupiane tym razem w odległości ROC, czyli dwukrotnie większej niż długość ogniskowa. Porównaj z Ryciną 39. 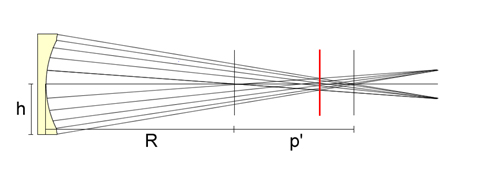 Rycina 41. Aberracja zwierciadła paraboidalnego w szczegółach. Ponieważ obraz w tym przypadku nie może być punktem, rozłożony jest wzdłuż pewnej przestrzeni, która jest wyolbrzymiona na ilustracji. Ma ona kształt trąbki, jej najwęższy przekrój to tzw. koło najmniejszej aberracji, zaznaczone czerwoną linią. Dotychczas mówiliśmy o promieniach skupionych w punktach, w rzeczywistości są to niewielkie koła. Dalej w tekście będę dla ułatwienia nadal odnosił się do punktu. Dzięki znajomości długości aberracji p' można przewidzieć i porównać teoretyczne wartości idealnego zwierciadła paraboidalnego i faktycznych pomiarów. (na podstawie Texereau [ 1 ]) Rodzaj deformacji określa wzór: 'p' = -b [(h2/R)+(h4/2R3)] Powyższego wzoru nie trzeba pamiętać. Najważniejsza jest w nim wartość b. Jeśli wynosi zero, zwierciadło ma kształt sferyczny, gdyż promienie skupiają się w jednym punkcie, nie istnieje więc aberracja podłużna (cały czas odnosimy się do blisko umieszczonego źródła światła). Deformacja o wartości -1 to parabola, ujemna wartość wskazuje, że promienie marginalne skupiają się dalej od zwierciadła niż promienie środkowe. Jeśli wartość b mieści się pomiędzy -1 i 0, figura ma kształt wycinka elipsy, inny rodzaj elipsy określony jest przez wartość b pomiędzy 0 i +1. Poniższa rycina przedstawia rodzaj deformacji powierzchni zwierciadła w zależności od wartości b. 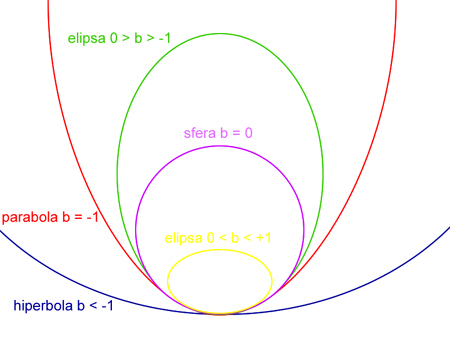 Rycina 42. Deformacja figury zwierciadła w zależności od wartości b (na podstawie Texereau [ 1 ]) Pisałem, że proces szlifowania zwierciadła jest jak nauka nowego rzemiosła. Czas więc na zbudowanie własnego narzędzia pomiarowego, zwanego nożem Foucaulta.
Przypisy: [ 1 ] Jean Texereau, How to Make a Telescope,
Second Edition, wydawnictwo Willmann-Bell, Inc., ISBN 0-943396-04-2. Wydawca
zezwala na reprodukcję, tłumaczenie i modyfikację ilustracji tylko na
zasadzie fair use, czyli w celach edukacyjnych i niedochodowych. Szczegóły
tego prawa można przeczytać w sekcjach 107 i 108 dokumentu United States
Copyright Act. « Budujemy własny teleskop (Publikacja: 12-06-2006 Ostatnia zmiana: 10-07-2007)
str. 4844 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [ Regulamin publikacji ] [ Bannery ] [ Mapa portalu ] [ Reklama ] [ Sklep ] [ Zarejestruj się ] [ Kontakt ] Racjonalista © Copyright 2000-2018 (e-mail: redakcja | administrator) | ||





 Ukończył biologię molekularną na Uniwersytecie Adama Mickiewicza w Poznaniu. Pracował jako Research Specialist in Health Science w Department of Anatomy and Cell Biology na University of Illinois w Chicago. Obecnie pracuje jako Associate Cell Biologist / Histologist w Abbott Laboratories (Illinois). Specjalizuje się w ekspresji białek 'od zera', hodowlach linii komórkowych, symulacji in vitro procesów zachodzących w komórkach. Jego pasją jest teoria ewolucji, w szczególności ewolucja systemów biochemicznych i pochodzenie życia we Wszechświecie.
Ukończył biologię molekularną na Uniwersytecie Adama Mickiewicza w Poznaniu. Pracował jako Research Specialist in Health Science w Department of Anatomy and Cell Biology na University of Illinois w Chicago. Obecnie pracuje jako Associate Cell Biologist / Histologist w Abbott Laboratories (Illinois). Specjalizuje się w ekspresji białek 'od zera', hodowlach linii komórkowych, symulacji in vitro procesów zachodzących w komórkach. Jego pasją jest teoria ewolucji, w szczególności ewolucja systemów biochemicznych i pochodzenie życia we Wszechświecie.