 |
         |
|
 |
Nauka » Astronomia » Budujemy własny teleskop Test Foucaulta i parabolizacja Budowa noża FoucaultaNóż Foucaulta to aparat, który posiada źródło światła w postaci diody LED, która może poruszać się na ramieniu wzdłuż i wszerz osi optycznej zwierciadła. (patrz Ryc. 43) Światło odbija się od zwierciadła i skupiane jest na ostrzu żyletki, również umieszczonej na tym samym ramieniu. Ramieniem można poruszać za pomocą pokręteł, przez co ruchy mogą być precyzyjne. Pokrętło wzdłużne posiada również podziałkę z dokładnością setnej części milimetra, która posłuży w późniejszej ocenie ilościowej zwierciadła. Poniższy aparat to jedna z wielu możliwości wykonania, jeszcze jakiś czas temu budowało się osobną komorę dla żarówki, jednak dziś wskaźniki posiadające diodę LED są tanie i powszechne. Należy zdecydować się, czy źródło światła będzie poruszać się wraz z nożem, czy też będzie nieruchome stało obok. Od tej decyzji zależą szczegóły wykonania i późniejszej oceny ilościowej zwierciadła. Osobiście namawiam na ruchome źródło światła, gdyż jest wygodniejsze i nie trzeba wykonywać szczeliny i równać jej z krawędzią noża. Należy pamiętać, aby żyletka i źródło światła znajdowały się w tej samej odległości od zwierciadła, oraz aby krawędź żyletki znajdowała się w połowie źródła światła.  Rycina 43. Podstawowe elementy noża Foucaulta. Aparat pomiarowy powinien być przytwierdzony do stabilnego podłoża. Wstawka pokazuje podziałkę widzianą od tyłu, w tym wypadku jeden obrót równa się 3 mm przesunięcia się noża wzdłuż osi optycznej. Numery powinny rosnąć wraz z oddalaniem się noża od zwierciadła. Żyletka musi poruszać się w dwóch płaszczyznach: wzdłuż i wszerz osi optycznej zwierciadła. Na stronie A Knife-edge Tester znajdziecie projekt aparatu z nieruchomym źródłem światła. Można też pogooglować w celu znalezienia innych pomysłów. Do kompletu pomiarowego potrzebna jest jeszcze podstawa dla zwierciadła, którą będzie można obracać i manipulować w pionie, aby poprawnie ustawić zwierciadło względem noża. Poniżej najbardziej prosta wersja, jaką można sobie wyobrazić, warto jest też dodać pokrętła na spodzie, aby móc regulować przechył.  Rycina 44. Podstawa pod zwierciadło. W części przedniej umieszczamy zwierciadło i przytwierdzamy je za pomocą kawałka taśmy dwustronnej. Z tyłu można położyć coś ciężkiego, aby zapobiec przewróceniu się zwierciadła do przodu. Przechył można regulować np. podkładając kartki pod część tylną. Test FoucaultaAby ustawić zwierciadło do oceny figury i pomiarów, należy je wpierw dobrze wyczyścić. Najlepiej spłukać je letnią wodą z kroplą płynu do mycia naczyń, po czym wysuszyć ręcznikiem papierowym. Powierzchnię przecieramy następnie chusteczką dezynfekującą nasączoną izopropanolem. Stawiamy zwierciadło na stojaku, dociskając jego tylną powierzchnię do kawałka taśmy dwustronnej, przytwierdzonego do ściany pionowej podstawy. Od powierzchni zwierciadła rozwijamy miarę i ustawiamy stolik z nożem Foucaulta w odległości jak najbliższej ROC. Warto mieć tutaj podwójny wskaźnik, zarówno z laserem, jak i diodą LED, ponieważ za pomocą lasera można o wiele łatwiej zgrać zwierciadło z nożem.  Rycina 45. Przygotowanie do pomiarów nożem Foucaulta. Stolik, na którym stoi nóż, musi być stabilny, a operator powinien siedzieć wygodnie tuż za nim. Na początku najłatwiej użyć lasera, aby znaleźć odbicie na krawędzi żyletki, potem można przełączyć na LED i przesuwając nóż w przód i w tył, odnaleźć ostry obraz. Po ustawieniu noża, gasimy światło w pomieszczeniu i siadamy z okiem umieszczonym tuż za żyletką. Powoli kręcimy pokrętłem poprzecznym, aż do momentu kiedy zobaczymy odbicie diody LED, które dotychczas było zasłonięte. Należy usiąść tak blisko, aby odbicie LED wypełniało jednolicie całą powierzchnię zwierciadła i nasze pole widzenia. Należy pozostać w tej pozycji nieruchomo i użyć ponownie pokrętła przesuwając żyletkę z powrotem, zasłaniając powoli promienie powracające. Sprawna obsługa noża Foucaulta wymaga długiej praktyki i cierpliwości. Lekkie szturchnięcie aparatu spowoduje konieczność ustawiania wszystkiego od nowa. Tutaj nie można się spieszyć, sam wiem jak bardzo może to być frustrujące, ale po pewnym czasie staje się rutyną i ustawianie noża jest kwestią niecałej minuty. Zanim przejdę do dostrajania noża w celu użycia, należy wytłumaczyć, co właściwie spodziewamy się zobaczyć. Dla ułatwienia załóżmy, że szczęśliwym trafem udało nam się wypolerować idealną sferę. Ustawiamy nóż Foucaulta nieco bliżej zwierciadła, czyli w odległości poniżej ROC. Jeśli krawędź noża zacznie wchodzić z lewej strony w promienie powracające, zobaczymy, że lewa strona zwierciadła staje się ciemna. Gdy nóż odsuniemy dalej, w odległość większą niż ROC, mimo że żyletka wędruje z lewej strony, ciemna staje się prawa strona zwierciadła! Jeśli zaś nóż wejdzie dokładnie w punkcie ROC, cała powierzchnia zwierciadła wygaśnie w tym samym momencie. Najprościej będzie to zrozumieć, jeśli spojrzycie na poniższą ilustrację. 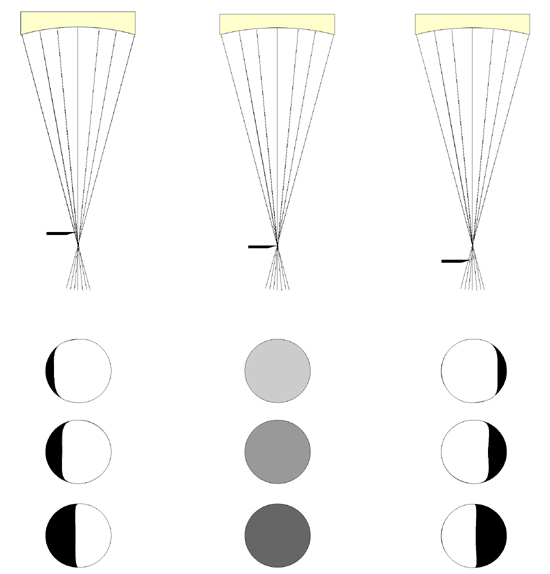 Rycina 46. Tak wygląda zwierciadło sferyczne badane za pomocą noża Foucaulta. (Porównaj z Ryc. 40) W tym przypadku krawędź żyletki zawsze wprowadzana jest z lewej strony obserwatora i odcina promienie dochodzące do oka, które znajduje się tuż za nożem. Jeśli odcinane są promienie w odległości bliższej niż ROC, cień na zwierciadle wędruje w tym samym kierunku co nóż (po lewej). Jeśli promienie odcinane są w odległości dalszej od ROC, cień na zwierciadle wędruje w kierunku przeciwnym do kierunku noża (po prawej). Kiedy krawędź noża wprowadzona zostanie dokładnie w punkcie ROC, zwierciadło zgaśnie jednakowo na całej powierzchni (środek). Na to specyficzne „wygaszenie" zwierciadła musimy wyczulić sobie oko — jego rozpoznanie jest podstawą zrozumienia figury zwierciadła i późniejszych pomiarów ilościowych. Wygaszenie jest jedynie zaciemnieniem zwierciadła, jednak nie staje się ono absolutnie czarne, tak jak w przypadku, gdy krawędź noża wchodzi poza punktem ROC. W tym momencie mogę wyjaśnić również jak prawidłowo ustawić aparat do pomiarów. Najbardziej istotną kwestią jest zrównanie osi przemieszczania się noża z osią optyczną zwierciadła. Po znalezieniu promienia odbitego ustawiamy krawędź noża nieco bliżej niż ROC i wprowadzamy w powracające światło aż do momentu, kiedy czarny cień będzie znajdował się na środku zwierciadła. Następnie przemieszczamy krawędź noża do siebie i obserwujemy cień. Jeśli cień pozostaje po środku, oznacza to, że krawędź wędruje wzdłuż osi optycznej zwierciadła i jesteśmy gotowi do pomiarów. Jeśli jednak cień wędruje dalej, zasłaniając coraz więcej powierzchni zwierciadła, należy odrobinę obrócić cały aparat zgodnie z wskazówkami zegara i ponownie powtórzyć powyższy test. Jeśli cień ucieka na zewnątrz, aparat należy przekręcić w kierunku przeciwnym do wskazówek zegara, aby zrównać obydwie osie. Jak zatem będzie wyglądać zwierciadło paraboidalne testowane nożem Foucaulta? Jak już wcześniej opisywałem promienie odbite z różnych części zwierciadła skupiane są w różnych punktach na osi optycznej. (porównaj Ryc. 40, Ryc. 41) Czyli jeśli wprowadzimy krawędź noża w każdy z tych punktów, jedynie część zwierciadła powinna ulec zaciemnieniu. I tak też to następuje. Poniższa rycina wyjaśnia analizę zwierciadła paraboidalnego za pomocą noża Foucaulta. 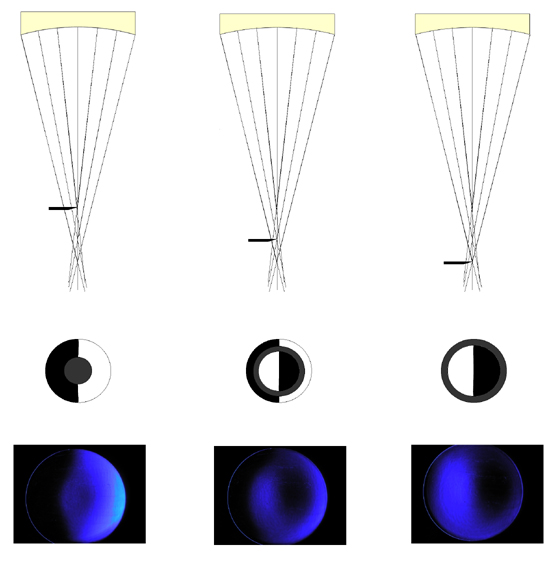 Rycina 47. Analiza zwierciadła paraboidalnego za pomocą noża Foucaulta, czyli „miska od spodu" — „obwarzanek" — „miska od góry". Wykresy na górze wskazują miejsce wprowadzenia krawędzi noża, po środku przedstawiony jest schematycznie obszar wygaszony (ciemnoszary kolor), na dole przykładowe zdjęcia z rzeczywistych obserwacji. Po lewej wygaszony zostaje środek, gdyż krawędź noża wchodzi w punkt, gdzie skupiane są promienie z obszaru środkowego. W następnym diagramie wygaszony zostaje obszar 0.7 średnicy zwierciadła, gdyż krawędź noża wchodzi w promienie skupiane z tego obszaru. Po prawej wygaszona zostaje krawędź. (Na podstawie Texereau [ 1 ]) Przestudiuj dokładnie powyższe wykresy, zanim rozpoczniesz pomiary i staraj się jak najlepiej zrozumieć istotę testu Foucaulta. Obserwowane obrazy najlepiej interpretować w następujący sposób. Wyobraź sobie, że z prawej strony zwierciadła stoi wyimaginowane źródło światła. Załóżmy również, że oświetlane przez nie przeszkody obiekty NIE rzucają cienia oraz NIE powstrzymują tego światła. Zapamiętaj i naszkicuj schematycznie profil jaki zauważyłeś, po czym użyj tabeli poniżej do interpretacji. Jeśli założymy, że szlifowanie i polerowanie zaszło idealnie i robiłeś wszystko prawidłowo, na samym końcu procesu powinieneś otrzymać sferę. Życie oczywiście nie jest takie proste i jako początkujący zapewne uzyskasz figurę, którą będzie trzeba poprawić. Pamiętaj jeszcze raz — jedyne zwierciadło, którego nie da się poprawić to takie, które roztrzaskało się o podłogę. Poniżej podaję przykłady figur i propozycje ich rozwiązania. 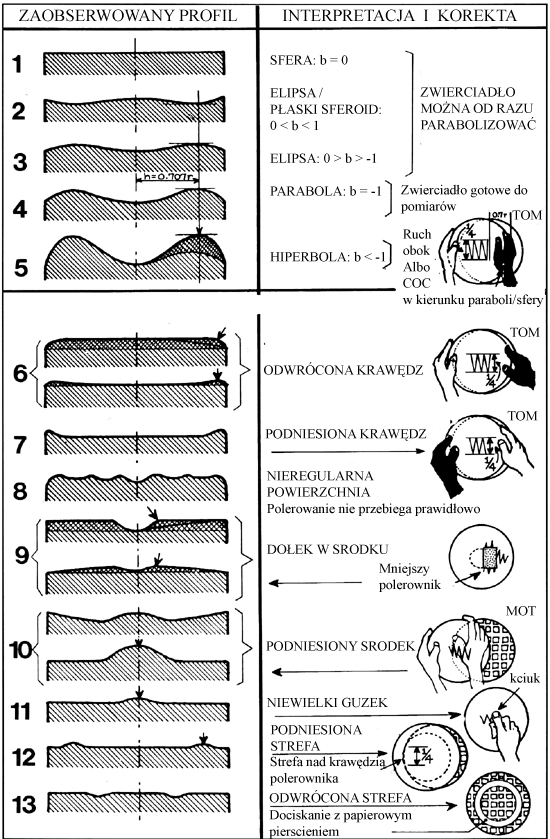 Rycina 48. Zaobserwowany profil za pomocą noża Foucaulta przekłada się na figurę zwierciadła. Jeśli wykonywałeś polerowanie zgodnie z wszystkimi regułami, bardzo możliwe, że uzyskasz jedną z figur oznaczonych od 1 do 5. Przykłady oznaczone od 6 do 13 są rzadsze i jeśli uzyskasz którykolwiek z nich, postaraj się kontynuować normalne polerowanie przez kolejne 2-3 godziny. Jeśli wada nie znika, staraj się zastosować przedstawioną powyżej korektę. (zmodyfikowane z Texereau [ 1 ]) Ja uzyskałem po polerowaniu płaski sferoid i chciałbym Was na tą figurę uczulić, gdyż można na początku pomylić ją z parabolą. Daje ona mianowicie taką samą sekwencję obrazów jak parabola, z tym że promienie środkowe są skupiane dalej niż promienie marginalne. Przyczyną są podniesiony środek i krawędzie. Czyli innymi słowy — nóż znajduje się bliżej zwierciadła, gdy wygaszona jest krawędź niż gdy wygaszony jest środek. Jeśli twoje zwierciadło ma kształt paraboidalny na samym początku, gratuluje szczęścia, będą potrzebne jedynie drobne poprawki. Jeżeli startujesz ze sfery, elipsy lub płaskiego sferoidu czas zapoznać się z następnym procesem. ParabolizacjaParabolizacja to proces powolny i należy wykonywać go z uwagą. Jedna sesja powinna obejmować jedynie 1-2 obrotów zwierciadła — należy zaznaczyć punkt, z którego startujemy i skończyć tuż przed nim. Ruch powinien być wolny — przekroczenie zwierciadła z jednej strony na drugą powinno trwać około 3 sekund. Zasięg ruchów parabolizacyjnych wynosi aż 4/5 średnicy zwierciadła i jego schemat jest pokazany poniżej. Po każdej sesji zwierciadło należy umyć, wysuszyć i przetestować. Kiedy po pewnym czasie zauważamy, że krawędź bądź środek zwierciadła wymaga większej redukcji, należy ruch parabolizacyjny nieco zmodyfikować, co przedstawione jest na ilustracji poniżej. 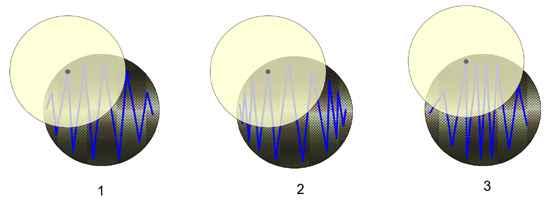 Rycina 49. Parabolizacja zwierciadła. Normalny ruch parabolizacyjny oznaczony jest cyfrą 1. Ruch pogłębiający środek (2) odznacza się częstszymi posuwami środka zwierciadła ponad krawędzią polerownika, ruch redukujący krawędź (3) polega na skupieniu się nad środkiem polerownika. (na podstawie Texereau [ 1 ]) Kiedy otrzymałeś figurę, która testowana nożem Foucalta pokazuje sekwencję obrazów jak na Rycinie 47, czas na dokładniejszą analizę zwierciadła. Odradzam wcześniejsze pomiary, gdyż na tym etapie możesz jeszcze nie potrafić przewidywać działania polerownika i skupianie się na pojedynczych strefach może doprowadzić jedynie do frustracji. Najlepszym sposobem jest uzyskanie wpierw prawidłowej figury, następnie przystąpienie do jej pomiarów.
Przypisy: [ 1 ] Jean Texereau, How to Make a Telescope,
Second Edition, wydawnictwo Willmann-Bell, Inc., ISBN 0-943396-04-2. Wydawca
zezwala na reprodukcję, tłumaczenie i modyfikację ilustracji tylko na
zasadzie fair use, czyli w celach edukacyjnych i niedochodowych. Szczegóły
tego prawa można przeczytać w sekcjach 107 i 108 dokumentu United States
Copyright Act. « Budujemy własny teleskop (Publikacja: 12-06-2006 Ostatnia zmiana: 17-06-2006)
str. 4845 |
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ukończył biologię molekularną na Uniwersytecie Adama Mickiewicza w Poznaniu. Pracował jako Research Specialist in Health Science w Department of Anatomy and Cell Biology na University of Illinois w Chicago. Obecnie pracuje jako Associate Cell Biologist / Histologist w Abbott Laboratories (Illinois). Specjalizuje się w ekspresji białek 'od zera', hodowlach linii komórkowych, symulacji in vitro procesów zachodzących w komórkach. Jego pasją jest teoria ewolucji, w szczególności ewolucja systemów biochemicznych i pochodzenie życia we Wszechświecie.
| [ Regulamin publikacji ] [ Bannery ] [ Mapa portalu ] [ Reklama ] [ Sklep ] [ Zarejestruj się ] [ Kontakt ] Racjonalista © Copyright 2000-2018 (e-mail: redakcja | administrator) | ||
 | ||