Autor tekstu: Sean M. Carroll

Tłumaczenie: Paulina Wojciechowska

Kim Body i ja właśnie napisaliśmy nową publikację, chyba z moim najbardziej ulubionym tytułem ze wszystkich prac:

Can the Higgs Boson Save Us From the Menace of the Boltzmann Brains? (Czy bozon Higgsa może uratować nas przed mrocznym widmem mózgu Boltzmanna?)
Kimberly K. Boddy, Sean M. Carroll
(Praca nadesłana 21.08.2013)

Standardowy model ΛCDM (*standardowy model kosmologiczny wszechświata z Wielkim Wybuchem, gdzie zakłada się istnienie we wszechświecie stałej kosmologicznej oznaczanej literą lambda i zimną ciemną materią, przyp. Tłum) doskonale pasuje do współczesnych obserwacji kosmologicznych, ale napotykamy w nim potencjalnie poważną kwestię mózgów Boltzmanna. Gdy wszechświat osiągnie fazę próżni de Sittera, która naprawdę trwa wiecznie, w pustej przestrzeni będzie panować skończona temperatura i odpowiadające jej fluktuacje. Tymi fluktuacjami będą m.in. inteligentni obserwatorzy, jak też konfiguracje, które odtworzą dowolny lokalny obszar obecnego wszechświata z dowolną dokładnością. W pracy omawiamy możliwość uniknięcia tej nieakceptowalnej sytuacji przy pomocy znanych praw fizyki: niestabilności próżni indukowanej polem Higgsa. Uniknięcie mózgów Boltzmanna w sposób niezależny od metryki wymaga skali czasu rozpadu rzędu obecnego wieku wszechświata, co można osiągnąć jeżeli masa efektywna kwarku t wynosi w przybliżeniu 178 GeV. W przeciwnym razie potrzebujemy nowych praw fizyki lub konkretnej metryki kosmologicznej, zanim będziemy mogli potraktować model ΛCDM jako sukces doświadczalny.

Stosujemy tu pewne szokujące pomysły do bardzo realistycznych praw fizyki. Między innymi, sugerujemy, że masa kwarka t może być większa niż się powszechnie sądzi oraz, że nasz wszechświat rozpadnie się w przeciągu około najbliższych 10 miliardów lat. Oto nieco rozwlekłe wyjaśnienie.

Małpy w pokoju (Infinite_monkey_theorem), uderzające w przypadkowe klawisze na maszynach do pisania, w końcu „wyprodukują" doskonałą kopię „Hamleta". Zakładając, oczywiście, że ich pisanina jest całkowicie przypadkowa oraz, że trwa to dostatecznie długo. Tak naprawdę potrzebny jest baaardzo długi okres czasu, o wiele większy niż obecny wiek wszechświata. Zatem jest to zabawny eksperyment myślowy, a nie realna propozycja tworzenia nowych dzieł literackich (albo starych).

Istnieje pewna interesująca cecha tego, co nasze małpy z eksperymentu myślowego stworzą. Załóżmy, że znajdziesz małpę, która właśnie napisała pierwszy akt „Hamleta" ze stuprocentową wiernością wobec oryginału Shakespeare’a. Pomyślisz może „aha, tak to się dzieje" I będziesz czekać na pojawienie się aktu drugiego jako następnego. Ale według warunków eksperymentu, to, co dalej napisze małpa, powinno być doskonale przypadkowe (przez co mamy na myśli, wybrane z jednorodnego rozkładu wśród wszystkich dozwolonych znaków typograficznych), a zatem niezależnych od tego, co pojawiło się wcześniej. Prawdopodobieństwo tego, że rzeczywiście pojawi się akt drugi tylko dlatego, że właśnie dostałeś akt pierwszy, jest nadzwyczaj małe. Na każde jedno zdarzenie, gdy twoje małpy napiszą dokładną wersję „Hamleta", napiszą ją nieprawidłowo olbrzymią liczbę razy — pojawią się małe błędy, duże błędy, wszystkie słowa ze sztuki, ale w przypadkowej kolejności, cały tekst od końca do początku, niektóre sceny, a inne nie, wszystkie wersy, ale wypowiadane przez inne postaci, itd. Zakładając, że jakiś fragment odpowiada wiernie oryginałowi, nadal jest ogromnie prawdopodobne, że fragmenty przed i po nim stanowią przypadkowy szum.

To jest, w pigułce, kwestia mózgów Boltzmanna (Boltzmanns anthropicbrain). Teraz zastąp swoje piszące na maszynach małpy pudełkiem atomów o określonej temperaturze i pozwól, by atomy te zderzały się przypadkowo ze sobą przez nieokreślony okres czasu. Przez większość czasu atomy będą w nieuporządkowanym stanie równowagi o wysokiej entropii. W końcu, całkiem przypadkiem, przybiorą postać uśmiechającej się buźki, Dawida Michała Anioła, lub absolutnie dowolnej konfiguracji, która jest kompatybilna z zawartością pudełka. Jeżeli poczekasz dostatecznie długo, a twoje pudełko jest dostatecznie duże, pojawi się w nim jakaś osoba, planeta, galaktyka, cały znany nam wszechświat (A universe out of chaos). Ale nawet wiedząc, że niektóre z atomów przybiorą jakiś dobrze ci znany układ, nadal oczekujemy, że pozostałe atomy będą w całkowicie przypadkowym ułożeniu. Innymi słowy, to, że znalazłeś kopię Mona Lizy, nie oznacza wcale, że została namalowana przez Leonarda da Vinci ani nikogo innego. Z ogromnym prawdopodobieństwem, po prostu obraz powstał stopniowo z przypadkowych ruchów atomów. Tylko dlatego, że to, co widzisz, wygląda jak fotografia, nie ma powodu przypuszczać, że faktycznie miało miejsce zdarzenie, które zdjęcie rzekomo reprezentuje. Jeśli przypadkowe ruchy atomów tworzą osobę z ugruntowanymi wspomnieniami przeszłości, wszystkie te wspomnienia są z bardzo dużym prawdopodobieństwem fałszywe.

Choć ten eksperyment myślowy był pierwotnie istotny, ponieważ sam Boltzmann (a przed nim Lukrecjusz — The first quantum cosmologist, Hume — Happy birthday David Hume, itd.) zasugerował, że nasz świat może być właśnie taki: wielkie pudło gazu, ewoluujące przez całą wieczność, z którego nasz obecny stan niskiej entropii wyłonił się jako przypadkowa fluktuacja. Jak zauważył Eddington, Feynman (Richard Feynman on Boltzmann brains), i inni, taki pomysł nie działa, z właśnie wymienionych powodów. Mając dany dowolny fragment wszechświata, który chciałbyś stworzyć (osobę, układ słoneczny, galaktykę, a nawet swoją dokładną kopię), reszta świata nadal powinna pozostawać w stanie maksymalnej entropii, a to przecież oczywiście nie ma miejsca. Kwestię tę określa się mianem „problemu mózgu Boltzmanna", ponieważ można wyobrażać sobie, że ogromna większość inteligentnych obserwatorów we wszechświecie to pozbawione ciał mózgi, które wyfluktuowały przypadkowo z otaczającego chaosu, a nie wyewoluowały w sposób konwencjonalny z przeszłości o niskiej entropii. To jednak nie stanowi głównej przeszkody. Prawdziwy problem polega na tym, że taki scenariusz fluktuacji jest poznawczo niestabilny (Boltzmann's universe ) — nie możesz równocześnie wierzyć, że jest prawdziwy i mieć zasadne powody, by wierzyć, że jest prawdziwy, ponieważ przewiduje on, że wszystkie „przyczyny", które uważasz za tak słuszne po prostu przypadkowo wyfluktuowały w twojej głowie.

Wszystko to zdawać by się mogło niczym więcej niż pożywką dla badaczy historii intelektualnej, teraz, gdy wiemy, że wszechświat nie jest wiecznym pudełkiem gazu. Obserwowalny wszechświat powstał zaledwie 13,8 miliarda lat temu, w Wielki Wybuchu o bardzo niskiej entropii. 13,8 miliarda lat wydaje się być długim okresem, ale czas potrzebny, by przypadkowe fluktuacje wytworzyły cokolwiek interesującego jest znacznie dłuższy. (Aby pojawiło się coś wysoce uporządkowanego z czegoś z entropią S, musisz poczekać przez okres czasu rzędu e^S. Ponieważ obiekty makroskopowe mają ponad 10^23 cząstek, S jest przynajmniej tej wielkości. Zatem mówimy o bardzo bardzo długich okresach czasu, tak długich, że nie zależy, czy czas mierzysz w mikrosekundach , czy miliardach lat). Poza tym, wszechświat nie jest pudłem gazu. Rozszerza się i opróżnia, prawda?

Ach, ale to wszystko jest trochę bardziej skomplikowane niż to, co powiedzieliśmy do tej pory. Dziś wiemy, że wszechświat nie tylko rozszerza się, ale także przyspiesza Dark energy ). Najprostszym wytłumaczeniem tego zjawiska — oczywiście nie jedynym — jest założenie, że pustą przestrzeń wypełnia stała wartość energii próżni, tzw. Stała kosmologiczna. Energia próżni nie zmniejsza się podczas rozszerzania się wszechświata. W zasadzie, nie istnieje nic, co powstrzymałoby wszechświat przed istnieniem wiecznym. Więc, nawet jeśli wszechświat istnieje od skończonego okresu czasu w przeszłości, nie ma przeszkód, by trwał wiecznie w przyszłości.

Ale, myślisz sobie, przecież wszechświat staje się coraz bardziej pusty gdy się rozszerza, więc nie pozostawia żadnych cząstek, które mogłyby fluktuować? Tylko do pewnego stopnia. Wszechświat z energią próżni przyspiesza wiecznie i w wyniku tego otacza nas kosmologiczny horyzont — obiekty, które znajdują się dostatecznie daleko, nigdy do nas nie dotrą, ani nawet nie prześlą informacji, ponieważ przestrzeń rozszerza się zbyt szybko. i, jak wykazali Stephen Hawking i Gary Gibbons w latach siedemdziesiątych ubiegłego stulecia, taka kosmologia jest analogiczna do czarnej dziury: z tym horyzontem będzie związane promieniowanie (Gibbons-Hawking effect), o stałej temperaturze.

Innymi słowy, wszechświat ze stałą kosmologiczną jest jak pudło gazu (o rozmiarach horyzontu), które trwa wiecznie ze stałą temperaturą. Co oznacza, że występują w nim przypadkowe fluktuacje. Gdy poczekamy dostatecznie długo, jakiś obszar wszechświata przefluktuuje w całkowicie każdą konfigurację materii spójną z lokalnymi prawami fizyki. W atomy, wirusy, ludzi, smoki, co tylko chcesz. Pokój, w którym jesteś teraz (albo atmosfera, jeśli jesteś na zewnątrz), zostanie zrekonstruowany do najdrobniejszych szczegółów, nieskończoną ilość razy w przyszłości. W ogromnej większości przypadków, kiedy twoje otoczenie zostaje odtworzone, reszta wszechświata będzie stanem równowagi o wysokiej entropii (w tym przypadku, pustą przestrzenią o niskiej temperaturze). Te wszystkie kopie ciebie będą sądzić, że mają prawdziwe wspomnienia przeszłości i dokładny obraz tego, jak wygląda świat, ale nie będą miały racji. A ty możesz być jedną z tych kopii.

To byłoby kiepskie.

Dyskusje o problemie Mózgu Boltzmanna zwykle pojawiają się w kontekście spekulacji takich, jak wieczna inflacja czy wieloświat (multiświat). (Nie, żeby było coś w tym złego). I, bądźmy uczciwi, sam pomysł uporządkowanych konfiguracji materii pojawiających się spontanicznie z otaczającego chaosu brzmi nieco zwariowanie, jak zauważają krytycy (patrz: Gibbons Hawking effect ). Ale wszystko, o czym właśnie powiedziałem, opiera się na fizyce, o której uważamy, że ją rozumiemy: na kwantowej teorii pola, ogólnej teorii względności i stałej kosmologicznej. Taki jest prawdziwy świat, koteczku/Nero. Oczywiście, być może popełniamy jakiś subtelny błąd w zrozumieniu, jak działa kwantowa teoria pola. To jednak jest bardziej spekulatywne niż poważne potraktowanie prostego wniosku płynącego z teorii.

Współcześni kosmolodzy mają ulubioną standardową teorię wszechświata, określaną mianem ΛCDM, gdzie „ Λ" oznacza stałą kosmologiczną, a „CDM" — "zimną ciemną materię" (Cold Dark Matter). Tutaj chcemy podkreślić, że ΛCDM, obecnie wiodąca teoria dokładnego opisu kosmosu, nie może sama być prawdziwa. Zawiera w sobie problem mózgu Boltzmanna i jest dlatego poznawczo/kognitywnie niestabilna, oraz nieakceptowalna jako teoria fizyczna.

Czy możemy uniknąć tych niepokojących wniosków? Jasne, „podkręcająć" trochę fizykę. Najprostszy sposób to przyjęcie, że energia próżni nie jest tak naprawdę stałą, np. wyobrażając sobie, że jest polem dynamicznym (kwintesencją/quintessence). Z tym jednak wiążą się inne problemy, związane z bardzo małymi parametrami precyzyjnego dostrojenia (The fine structure constant is probably constant ) . W bardziej solidnym scenariuszu można by przywołać rozpad próżni kwantowej (Are many worlds and the multiverse the same idea ). Być może energia próżni jest przejściowo stała, ale istnieje inny stan próżni w przestrzeni pola z jeszcze niższą energią, do którego dokonamy pewnego dnia przejścia. Co by się wtedy działo? Maleńkie bąbelki konfiguracji o niższej energii zaczęłyby pojawiać się poprzez tunelowanie kwantowe. Bąbelki rosłyby gwałtownie z szybkością światła. Jeżeli energia innego stanu próżni wynosiłaby zero lub była ujemna, nie musielibyśmy uporać się z tym piekielnym problemem mózgu Boltzmanna.

Wspaniale, ale wydaje się, że wymaga to zastosowania spekulatywnej fizyki, w postaci nowych pól i nowego stanu próżni kwantowej. Czy istnieje jakikolwiek sposób, by uratować ΛCDM całkowicie bez nowych praw fizyki?

Odpowiedź na to pytanie — być może! Tutaj wkraczamy Kim i ja, choć niektóre pojedyncze elementy naszej układanki zostały wcześniej złożone przez innych autorów. Pierwszy element to interesujący fragment fizyki, który powalił media na początku tego roku: możliwość tego, że pole Higgsa podtrzymuje inny stan próżni (How the Higgs boson might spell doom for the universe) niż ten, w którym jesteśmy. (Powód, dla którego jest to prawdziwe, jest dość subtelny, ale sprowadza się do efektów grupy renormalizacyjnej (How quantum field theory becomes effective). Tak, tak: bez nowych praw fizyki jest możliwe, że pole Higgsa rozpadnie się w przyszłości przez „zarodkowanie bąbelków", co dramatycznie zmieni fizykę naszego wszechświata. Powodem, dla którego Higgs jest interesujący, jest to, że posiada niezerową wartość nawet w pustej przestrzeni. Tu mówimy, że wartość ta może być nawet większa przy nawet niższej energii. Jeszcze nie osiągnęliśmy tego stanu, ale moglibyśmy poprzez przejście fazowe. I, jak Kim i ja podkreślamy, to mogłoby uratować nas przed problemem mózgu Boltzmanna.

Wyobraź sobie, że wykres „energii pustej przestrzeni" wobec „wartości pola Higgsa" wygląda następująco: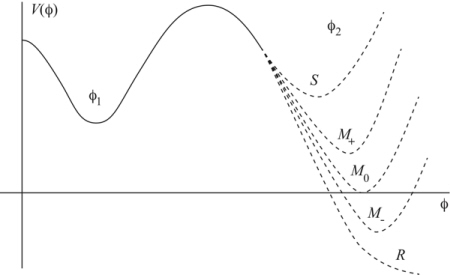

φ jest wartością pola Higgsa. Nasze obecne położenie to φ₁, gdzie jest trochę dodatniej energii. Gdzieś indziej o wiele większa wartość φ₂, z inną energią. Jeśli energia przy φ₂ jest większa niż φ1, nasza obecna próżnia jest stabilna. Jeżeli na jakąkolwiek niższą wartość, jesteśmy „metastabilni" — nasza obecna sytuacja może trochę potrwać, ale w końcu dokonamy przejścia do innego stanu. Albo Higgs nie może mieć innej próżni, rozwiązania „odległego". (Zauważ, że jeżeli energia w innym stanie jest ujemna, przestrzeń wewnątrz bąbelków nowej próżni ulegnie w rzeczywistości przejściu do stanu Wielkiego Kolapsu, zamiast dalszego rozszerzania się).

Ale nawet jeśli to jest prawda i tak mamy za mało informacji. Wyobraź sobie, że istnieje inny stan próżni i że możemy „zarodkować" bąbelki, które tworzą obszary nowej fazy. Bąbelki będą rozszerzać się prawie z szybkością światła — ale czy będą zderzać się z innymi bąbelkami i dojdzie do przejścia z naszej obecnej fazy do nowej? Innymi słowy, czy przejście będzie perkolować? Odpowiedź brzmi „tak", gdy bąbelki tworzą się odpowiednio szybko. Jeżeli tworzą się zbyt wolno, do gry włączą się kosmiczne horyzonty — czasoprzestrzeń rozszerza się tak szybko, że dwa przypadkowe bąble nigdy się nie spotkają, a objętość przestrzeni pozostałej w pierwotnej fazie (tej, w której jesteśmy teraz) będzie rosła bez ograniczeń. (Jest to tzw. „problem taktownego wyjścia" w scenariuszu wszechświata Alana Gutha).

Mając zatem dane, że pole Higgsa może podtrzymywać inną próżnię kwantową, pojawiają się dwa pytania. Po pierwsze, czy nasza próżnia jest stabilna, czy też istnieje faktycznie próżnia o niższej energii, do której możemy dokonać przejścia? Po drugie, jeżeli istnieje próżnia o niższej energii, czy nasza próżnia rozpada się dostatecznie szybko, tak, by przejście fazowe perkolowało, czy też pozostajemy z wiecznie rosnącą przestrzenią w obecnej fazie?

Odpowiedzi zależą od dokładnych wartości parametrów określających Model Standardowy fizyki cząstek elementarnych, a zatem określają zrenormalizowany potencjał Higgsa. W szczególności istotne są dwa parametry: masa samego Higgsa i masa kwarka t. Zmierzyliśmy obie te wielkości, ale oczywiście nasze pomiary mają skończoną dokładność. Na szczęście, odpowiedzi na oba te pytania (nasza próżnia jest stabilna i rozpada się dostatecznie szybko, by perkolować) zostały obliczone przez inne grupy badaczy: kwestią stabilności zajęła się (ostatnio, po o wiele wcześniejszych pracach) grupa Buzatto, zaś kwestią perkolacji — grupa Arkaniego-Hameda. Poniżej znajdują się odpowiedzi na wykresie w przestrzeni parametrycznej zdefiniowanej przez masę Higgsa i masę kwarku t. (Linie przerywane przedstawiają niepewność w pomiarach innego parametru, stałej sprzężenia chromodynamiki kwantowej).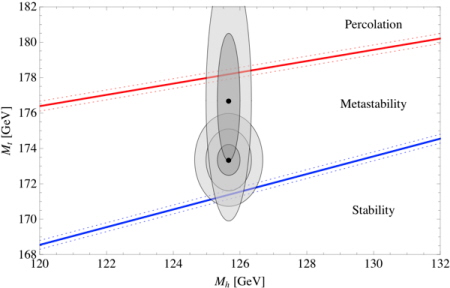

Percolation = perkolacja, Metastability = metastabilność, Stability = stabilność

Interesują nas dwie ukośne proste. Jeśli znajdujesz się poniżej dolnej prostej, pole Higgsa jest stabilne i masz zdecydowanie problem Mózgów Boltzmanna. Jeżeli znajdujesz się pomiędzy prostymi, bąble zarodkują i rosną, ale nie perkolują, i nasz obecny stan pozostaje bez zmian. (Patrz poniżej na odpowiedź, czy problem Mózgu Boltzmana jest wówczas uzależniony od pomiaru/miary). Gdy jesteś powyżej górnej prostej, bąble dosyć szybko zarodkują, a przejście dosyć dobrze perkoluje. Jednakże w tym obszarze bąble de facto zarodkują zbyt szybko — przejście fazowe już powinno było mieć miejsce!Preferowana część wykresu to właśnie sama górna ukośna prosta. Jest to jedyny obszar, w którym możemy zdecydowanie uniknąć Mózgów Boltzmanna, ale nadal prowadzić tę rozmowę.

Wykreśliliśmy także dwa zbiory elips, odpowiadających zmierzonym wartościom mas Higgsa i kwarka t. Według najnowszych obliczeń LHC (Large Hadron Collider), masa Higgsa wynosi 125,66 ± 0,34 GeV, co jest całkiem dobrą dokładnością. Zgodnie z najnowszymi obliczeniami, masa kwarka t wynosi 173,20 ± 0,87 GeV. Połączenie tych wyników daje dolny zbiór elips, gdzie zaznaczyliśmy kontury jednej sigmy (Thanksgiving), dwóch i trzech sigm. Widzimy, że środkowa wartość znajduje się w obszarze „metastabilnym", gdzie może dojść do zarodkowania bąbli, ale przejście fazowe jest zbyt wolne, by zaszła jego perkolacja. Jednakże słupki błędów sięgają do obszaru stabilnego.

Co ciekawe, pojawiły się pewne kontrowersje co do tego, czy zmierzona wartość masy kwarka t jest taka sama, jak parametr, którego używamy przy obliczeniach energii potencjalnej pola Higgsa (tzw. masa „efektywna"). Jest to dyskusja trochę poza moją dziedziną, ale w niedawnej publikacji (Thanksgiving-6) pracowników CMS próbowano dokonać pomiaru wielkości, jakiej faktycznie chcemy, i udało się to zrobić przy wiele większym odchyleniu standardowym 176,7 ± 3,6 GeV. Z pracy tej właśnie pochodzi nasz drugi zbiór elips (z jedną sigmą i z dwiema sigmami). Jeśli przyjmiemy te wyniki jako wartość nominalną, istnieje możliwość, że masa kwarka t wynosi 178 GeV, co wystarczałoby, by „mieszkać na linii życia", gdzie przejście fazowe zajdzie szybko, ale nie za szybko. Założę się, że pomiary są bliskie rzeczywistości, ale powiedzmy sobie tak: przewidujemy, że albo masa efektywna kwarka t de facto wynosi 178 GeV, albo istnieją jakieś nowe prawa fizyki, które włączają się i doprowadzają do destabilizacji naszej obecnej próżni.

Nie byłem pewien, co dzieje się w ogromnym obszarze „metastabilności", pomiędzy stabilnością i perkolacją. Bo tak naprawdę sytuacja jest nie do końca jasna. Naiwnie można stwierdzić, że w tym obszarze objętość przestrzeni w naszej obecnej próżni rośnie bez ograniczeń i zdominują ją Mózgi Boltzmanna. Ale analogiczna sytuacja wyłania się przy wiecznej inflacji, prowadząc do czegoś, co określamy mianem problemu metryki kosmologicznej . Celem naszej pracy nie było samo przedstawienie wykresów kilku krzywych, które wyliczyli inni badacze, ale próba zastosowania problemu metryki wiecznej inflacji do naszej rzeczywistości. Wyniki nie do końca rozstrzygnęły sytuację. W większości metryk, możemy powiedzieć to ze spokojem, problem Mózgu Boltzmanna jest tak trudny, jak mogłeś się obawiać. Ale istnieje przynajmniej jedna metryka — jeśli musisz wiedzieć, określamy ją mianem modyfikowanej metryki przyczynowej obszaru („modified causal-patch measure") z czasowymi próżniami — gdzie problemu Mózgu Boltzmanna można uniknąć. Nie jestem pewien, czy istnieje uzasadniona przyczyna, by wierzyć w tę metrykę, inna niż „daje nam ona akceptowalną odpowiedź", ale nasze wyniki sugerują, że zrozumienie kosmologicznej teorii metryki może być istotne, nawet jeśli nie wierzysz w wieczną inflację.

Ostatnia, prowokacyjna obserwacja, którą zachowałem na sam koniec. Najbezpieczniej jest znaleźć się na górnej poprzecznej prostej na naszym wykresie, gdzie mamy bąble zarodkujące dostatecznie szybko, by perkolować, ale nie tak szybko, by proces ten już zaszedł. Co zatem oznacza stwierdzenie „dostatecznie szybko, by perkolować"? Cóż, w przybliżeniu oznacza to, że bąble powinny powstawać w przybliżeniu raz na obecny wiek naszego wszechświata. (Don Page dokonał nieco dokładniejszego oszacowania — 20 miliardów lat). Z jednej strony, to JEST całkiem sporo miliardów lat - nie musimy spieszyć się z wykupieniem polisy ubezpieczeniowej. Z drugiej, to wcale nie jest aż tak długo. Oznacza to, że w przybliżeniu wszechświat osiągnął połowę swojego maksymalnego wieku. A przejście mogłoby zdarzyć się o wiele szybciej — być może jutro albo za rok, chociaż szanse na to są bardzo małe.

Aby uniknąć problemu Mózgów Boltzmanna, chcemy, by przejście zaszło szybko. Co zabawne, większość istniejącej litratury z dziedziny fizyki cząstek elementarnych odnośnie rozpadu pola Higgsa przyjmuje, że powinniśmy pragnąć, by było ono całkowicie stabilne — w przeciwnym razie rozpad Higgsa zniszczy wszechświat! To prawda, ale chcemy tu podkreślić, że jest to cecha, a nie „wirus", ponieważ musimy zniszczyć wszechświat (a przynajmniej stan, w jakim obecnie się znajduje), aby uchronić się przed inwazją Mózgów Boltzmanna.

Wszystko to, oczywiście, pod warunkiem, że przy wyższych energiach nie pojawiają się nowe prawa fizyki, które zmieniłyby nasze obliczenia, co wydaje się mało prawdopodobnym założeniem. Mamy zatem następujące alternatywy: nowe prawa fizyki, udoskonalone zrozumienie problemu metryki kosmologicznej albo przewidywanie, że kwark t ma naprawdę 178 GeV. Tak czy siak, wygrywamy.

The Higgs boson vs Boltzmann brains.

Sean Carroll/Preposterousuniverse, 22 sierpnia 2013r.

Dodaj komentarz do strony..   Zobacz komentarze (31)..

Wyślij mailem..

Wersja do druku    PDF    MS Word

Sean M. Carroll Fizyk teoretyk z California Institute of Technology w Pasadenie. W swoich badaniach zajmuje się teoretycznymi aspektami kosmologii, teorią pola, grawitacją I mechaniką kwantową. Napisał kilka książek popularno-naukowych, m.in. “Stąd do wieczności i z powrotem”, “The Particle at the End of the Universe: How the Hunt for the Higgs Boson Leads Us to the Edge of a New World”. Napisał także podręcznik dla studentów fizyki “Spacetime and Geometry: An Introduction to General Relatvity”, a także nagrał wykłady dla Teching Company “Dark Matter and Dark Energy” i “Mysteries of Time”.  Strona www autora  Liczba tekstów na portalu: 2  Pokaż inne teksty autora  Poprzedni tekst autora: Dlaczego (niemal wszyscy) kosmologowie są ateistami